Liczby pierwsze to niezwykłe obiekty matematyczne, które fascynują zarówno amatorów, jak i profesjonalnych matematyków. Są to liczby naturalne większe od 1, które mają dokładnie dwa dzielniki: 1 oraz samą siebie. Dzięki swojej unikalnej właściwości, liczby pierwsze odgrywają fundamentalną rolę w matematyce i są kluczowe dla wielu zastosowań praktycznych, w tym w kryptografii. Badanie liczb pierwszych prowadzi do wielu interesujących zagadek i problemów, takich jak hipoteza Riemanna, która wciąż czeka na swoje rozwiązanie. Zrozumienie tych zagadnień nie tylko rozwija naszą wiedzę, ale także ma realne znaczenie w codziennym życiu, co czyni temat liczb pierwszych bardzo aktualnym i wartym zgłębiania.
Kluczowe wnioski- Liczby pierwsze to liczby, które mają tylko dwa dzielniki: 1 i samą siebie.
- Podstawowe twierdzenie arytmetyki mówi, że każda liczba naturalna większa od 1 jest iloczynem liczb pierwszych.
- Hipoteza Riemanna dotyczy rozkładu liczb pierwszych i jest uznawana za jeden z najważniejszych problemów milenijnych.
- Liczby pierwsze mają kluczowe zastosowanie w kryptografii, szczególnie w algorytmie RSA.
- Badania nad liczbami pierwszymi przyciągają uwagę zarówno naukowców, jak i pasjonatów matematyki.
Definicja liczb pierwszych i ich kluczowe cechy
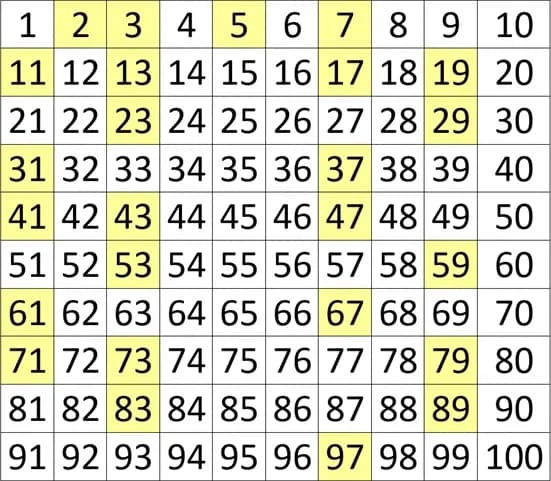
Liczby pierwsze to podstawowy temat w matematyce, który budzi wiele zainteresowania. Zdefiniować je można jako liczby naturalne większe od 1, które mają dokładnie dwa dzielniki: 1 oraz samą siebie. Przykłady liczb pierwszych to: 2, 3, 5, 7, 11, 13, 17, 19.
| Liczba | Typ |
|---|---|
| 2 | pierwsza |
| 3 | pierwsza |
| 5 | pierwsza |
| 7 | pierwsza |
Historia liczb pierwszych: od starożytności do współczesności
Liczby pierwsze mają długą historię, sięgającą czasów starożytnych, gdy naukowcy zaczęli je badać. Już Pitagorejczycy uważali je za „atomy” liczb, które są podstawą wszystkich innych liczb.
Współcześnie, badania nad liczbami pierwszymi przynoszą nowe odkrycia. Zastosowanie nowoczesnych technologii pozwala matematykom na lepsze zrozumienie ich właściwości oraz odkrywanie nowych liczb pierwszych.
Czytaj więcej: Zagadki lateralne - 5 zasad ich rozwiązywania i praktyczne przykłady
Podstawowe twierdzenia arytmetyki dotyczące liczb pierwszych
Jednym z najistotniejszych twierdzeń związanych z liczbami pierwszymi jest podstawowe twierdzenie arytmetyki. Mówi ono, że każdą liczbę naturalną większą od 1 można jednoznacznie przedstawić jako iloczyn liczb pierwszych. To twierdzenie podkreśla rolę liczb pierwszych w budowaniu innych liczb. Oto kilka kluczowych twierdzeń o liczbach pierwszych:
- Każda liczba naturalna większa od 1 ma jedną unikalną faktoryzację na liczby pierwsze.
- Nie ma największej liczby pierwszej; zawsze można znaleźć kolejną.
- Rozkład liczb pierwszych staje się coraz rzadszy w miarę wzrostu wartości liczb.
Dlaczego liczby pierwsze są fundamentem matematyki?

Liczby pierwsze pełnią kluczową rolę w teorii liczb. Oprócz ich podstawowej roli w faktoryzacji, mają również znaczenie w dowodach i hipotezach matematycznych, które wpływają na wiele innych dziedzin. Bez zrozumienia liczb pierwszych nie byłoby możliwe zbudowanie bardziej złożonych teorii matematycznych.
W innych dziedzinach matematyki, takich jak algebra, liczby pierwsze przyczyniają się do rozwoju teorii pierścieni i pól. Ich unikalne właściwości są wykorzystywane w badaniach nad liczbami całkowitymi i liczbami nieskończonymi.
Hipoteza Riemanna: tajemnica liczb pierwszych
Hipoteza Riemanna to jedna z najbardziej fascynujących i najbardziej trudnych do rozwiązania zagadek związanych z liczbami pierwszymi. Sformułowana przez Bernharda Riemanna w 1859 roku, dotycząca rozkładu liczb pierwszych, sugeruje istnienie wzoru, który opisuje to rozmieszczenie. Hipoteza ta jest kluczowa dla zrozumienia wielu aspektów teorii liczb, a jej rozwiązanie może mieć wpływ na wiele dziedzin, w tym kryptografię. Przyciąga ona uwagę matematyków na całym świecie.
Aktualne badania nad hipotezą Riemanna i ich znaczenie
Dziś trwają intensywne badania nad hipotezą Riemanna, które mają na celu znalezienie dowodu lub obalenie tego twierdzenia. Wiele prób dowodu zostało podjętych, jednak żadna z nich nie została uznana przez społeczność matematyczną. Przełomowe badania mają potencjał, aby zmienić zrozumienie rozkładu liczb pierwszych i ich roli w matematyce, co czyni tę hipotezę przedmiotem dużego zainteresowania.
Każde nowe odkrycie w tej dziedzinie może wpłynąć na rozwój algorytmów kryptograficznych oraz rozwiązań w teorii liczb. Dlatego matematycy nadal z pasją badają tę kwestię.
Zastosowania liczb pierwszych w kryptografii i zabezpieczeniach
Liczby pierwsze odgrywają kluczową rolę w kryptografii, zwłaszcza w systemach szyfrowania opartych na algorytmach takich jak RSA. To właśnie na ich unikalnych właściwościach opiera się bezpieczeństwo komunikacji w sieci. Ponadto, liczby pierwsze są wykorzystywane w protokołach zabezpieczających transakcje internetowe. Oto kilka przykładów zastosowania liczb pierwszych:
| Zastosowanie | Opis |
|---|---|
| Algorytm RSA | Używa faktoryzacji liczb pierwszych do tworzenia kluczy. |
| Bezpieczeństwo danych | Oparte na trudności rozkładu liczb na czynniki pierwsze. |
| Protokół SSL | Wykorzystuje liczby pierwsze do szyfrowania połączeń. |
Liczby pierwsze w informatyce: algorytmy i szyfrowanie
W informatyce, liczby pierwsze są wykorzystywane w algorytmach, które zapewniają bezpieczeństwo danych. Na przykład, w algorytmie RSA, ich jedyną rolą jest ochrona informacji. Dzięki ich właściwościom, są doskonałe do tworzenia kluczy szyfrujących oraz do zabezpieczania komunikacji między użytkownikami.
Oprócz kryptografii, liczby pierwsze mają również zastosowanie w badaniach algorytmicznych. Ich unikalne cechy sprawiają, że są one interesujące w kontekście analizy danych i optymalizacji algorytmów, co znacznie wpływa na wydajność obliczeń.
Ciekawe problemy i zagadki związane z liczbami pierwszymi
Licząc zagadka liczb pierwszych, spotykamy wiele interesujących problemów matematycznych, które skłaniają do głębszego rozważania. Oto kilka z nich:
- Czy istnieje nieskończona ilość liczb pierwszych?
- Jakie są rozkłady liczb pierwszych wśród liczb całkowitych?
- Jakie są najstarsze znane liczby pierwsze?
- Czy istnieje prosty sposób na obliczenie n-tej liczby pierwszej?
Zaskakujące fakty o liczbach pierwszych, które mogą zaintrygować
Warto wiedzieć, że liczby pierwsze są fascynującym tematem nie tylko dla matematyków, ale także dla każdego, kto lubi wyzwania intelektualne. Na przykład, największa znana liczba pierwsza ma ponad 24 miliony cyfr, co czyni ją niesamowitą w skali!
Innym zaskakującym faktem jest to, że liczba 2 jest jedyną liczbą pierwszą, która jest parzysta. Wszystkie inne liczby pierwsze są nieparzyste, co czyni tę cechę wyjątkową. Badania nad liczbami pierwszymi ciągle przynoszą nowości; być może czeka na nas jeszcze wiele odkryć.
Zrozumienie liczb pierwszych kluczem do matematycznych tajemnic
Liczby pierwsze są fundamentem, na którym opiera się wiele teorii matematycznych oraz zastosowań praktycznych. To dzięki nim możliwe jest zrozumienie złożonych zagadnień, takich jak hipoteza Riemanna czy unikalne zastosowania w kryptografii. Odkrycia dotyczące liczb pierwszych nie tylko wzbogacają teorię liczb, ale także mają realny wpływ na bezpieczeństwo danych w nowoczesnym świecie.
Artykuł pokazuje, że badania nad liczbami pierwszymi mają długą historię, która sięga starożytności, a ich aktualne znaczenie jest niewspółmiernie duże. Liczby te są nie tylko interesujące w kontekście matematycznym, ale także praktycznym, co wskazuje na ich rolę w codziennym życiu, zwłaszcza w kontekście szyfrowania i ochrony informacji. Dodatkowo, zrozumienie ich właściwości otwiera drzwi do wielu fascynujących zagadek, które mogą stanowić inspirację dla przyszłych pokoleń matematyków.
Podsumowując, liczby pierwsze są nie tylko obiektem badań matematycznych, ale również kluczem do zrozumienia bardziej skomplikowanych zagadnień i problemów. Ich unikalne cechy oraz tajemnice, które wciąż pozostają do odkrycia, sprawiają, że temat ten pozostaje aktualny i niezwykle inspirujący dla miłośników matematyki i technologii.