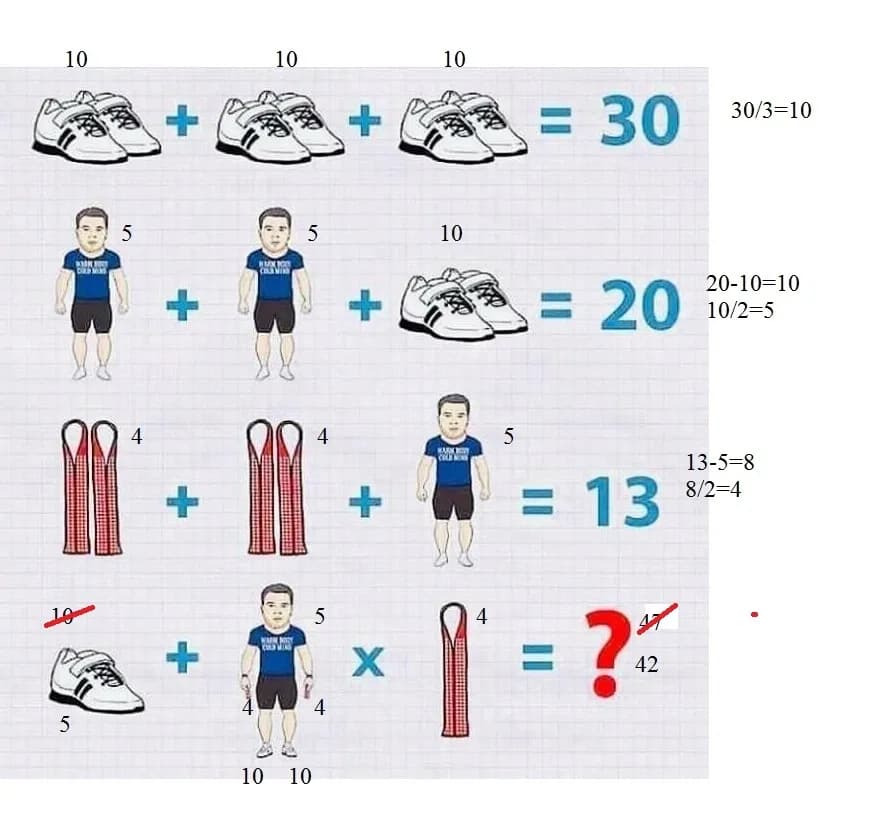
- Zagadka opiera się na pozornym braku złotówki w obliczeniach związanych z pożyczkami i wydatkami.
- Analiza sytuacji pokazuje, że mylenie sposobu zestawienia kwot prowadzi do błędnych wniosków.
- Przykład zakupu książki i zamówienia pizzy ilustruje mechanizm tej zagadki w różnych kontekstach.
- Krytyczne myślenie i zrozumienie matematyki są kluczowe dla uniknięcia takich pułapek.
- Warto przyjrzeć się, jak prezentacja danych wpływa na nasze postrzeganie problemów matematycznych.
Opis zagadki dotyczącej brakującej złotówki i jej kontekstu
Zagadka z brakującą złotówką to popularna łamigłówka matematyczna, która wprowadza w błąd wielu ludzi, prowadząc do mylnego wniosku o "brakującej" złotówce. Klasyczna wersja tej zagadki przedstawia sytuację, w której osoba, chcąc kupić książkę, pożycza pieniądze od rodzeństwa. Po zakupie, wydaje się, że istnieje różnica, której nie da się wyjaśnić.
| Kwota pożyczona | Kwota wydana | Reszta | Dług pożyczony |
| 50 zł (25 zł od siostry i 25 zł od brata) | 47 zł (na książkę) | 3 zł (reszty) | -50 zł (dług) |
Analiza błędów w rozumowaniu przy rozwiązaniu zagadki
Powszechną przyczyną mylnych wniosków w zagadka z brakującą złotówką jest błędne zestawienie kwot. Ludzie często myślą, że reszta powinna być dodawana do pozostałej kwoty, co prowadzi do niepoprawnych obliczeń. W rzeczywistości, należy jasno rozgraniczyć dług i posiadane pieniądze, aby zrozumieć całą sytuację.
Logiczne niedociągnięcia są często wynikiem zbyt uproszczonego myślenia. Osoby analizujące zagadkę pomijają kluczowe elementy, takie jak dług, przez co dochodzi do błędnych konkluzji. Istotne jest, aby zrozumieć, że pozostała złotówka nie powinna być dodawana do długów, lecz traktowana jako część zobowiązania wobec rodzeństwa.
Czytaj więcej: Kartkówka Alkany - Przykładowe zadania i odpowiedzi
Dlaczego brakująca złotówka jest mylona w rachunkach?
Wiele osób myli się, ponieważ nie rozumie, jak działa zasada dodawania i odejmowania w kontekście pożyczek i wydatków. Istnieje kilka powszechnych pomyłek, które mogą prowadzić do powstania iluzji "brakującej" złotówki:
- Nie uwzględnienie długu przy obliczeniach.
- Łączenie kwot, które nie powinny być sumowane.
- Potraktowanie ułamków kwot w sposób, który prowadzi do niejasności.
- Pomylenie reszty z pozostałym długiem.
Jak zrozumieć strukturę zagadki z brakującą złotówką?

Aby zrozumieć strukturę zagadka z brakującą złotówką, warto przeanalizować jej założenia. Kluczem jest zrozumienie, jak poszczególne elementy finansowe są ze sobą powiązane. Diagram ilustrujący te aspekty pomoże wizualizować relacje między długiem a posiadanymi pieniędzmi, co jest kluczowe dla właściwego zrozumienia.
Wersje zagadki z pizzą i inne przykłady łamigłówek matematycznych
Inna wersja tej zagadki występuje w kontekście trzech przyjaciół zamawiających pizzę. Koszt pizzy wynosi 30 zł, a każdy z przyjaciół płaci po 10 zł. Po obniżeniu ceny do 25 zł, kelner oddaje im po 1 zł i zatrzymuje 2 zł jako napiwek, co prowadzi do podobnej niejasności dotyczącej pieniędzy.
Inne interesujące łamańce językowe i zagadki matematyczne bazują na mylnych założeniach dotyczących wartości, które może prowadzić do zabawnych, ale mylących sytuacji. Przykłady takie jak "trzech przyjaciół" przedstawiają, jak łatwo można się pogubić w liczbach, co czyni te zagadki fascynującymi.
Porady dotyczące krytycznego myślenia w matematyce
Krytyczne myślenie jest niezbędne w rozwiązywaniu zagadek matematycznych. Ważne jest, by nie dać się zwieść pierwszemu wrażeniu i dokładnie analizować każdą sytuację. Warto zadawać pytania i weryfikować założenia, ponieważ wiele problemów matematycznych można rozwiązać, korzystając z analizy i logiki.Jak wizualizacje mogą pomóc w zrozumieniu zagadki?
Wizualizacje są kluczowym narzędziem w zrozumieniu zagadka z brakującą złotówką. Dzięki nim można łatwiej zobaczyć relacje między długiem, wydatkami oraz resztą pieniędzy. Tabela przedstawiająca różne typy wizualizacji może wskazać, jak graficzne przedstawienie danych wpływa na nasze myślenie.
| Rodzaj wizualizacji | Opis |
| Diagramy przepływu | Ilustrują przepływ pieniędzy i długów. |
| Wykresy słupkowe | Pomagają w porównaniu wydatków i reszt. |
| Schematy blokowe | Pokazują relacje między różnymi elementami finansowymi. |
Przyczyny powszechnych pułapek w myśleniu matematycznym
Psychologiczne aspekty myślenia matematycznego mogą prowadzić do popełniania błędów. Często ludzie mylnie zakładają, że ich intuicja jest wystarczająca do rozwiązania problemów, co prowadzi do błędnych konkluzji. Ważne jest, aby pamiętać, że matematyka opiera się na precyzyjnych zasadach, które powinny być przestrzegane.
Praktyczne skutki tych pułapek są różnorodne. Mogą one prowadzić do problemów w codziennych sytuacjach finansowych, takich jak planowanie budżetu czy dokonywanie obliczeń. Zrozumienie, jak unikać tych pułapek, może w znaczący sposób poprawić nasze umiejętności matematyczne i finansowe.
Zastosowanie zagadki w edukacji matematycznej
Zagadka z brakującą złotówką ma ogromne znaczenie w edukacji matematycznej. Można ją wykorzystywać do rozwijania umiejętności krytycznego myślenia oraz analizy logicznej u uczniów. W praktyce stosuje się ją do nauczania skomplikowanych pojęć matematycznych, a także jako narzędzie do doskonalenia umiejętności rozwiązywania problemów.
- Umożliwia uczniom zrozumienie podstawowych zasad matematyki.
- Pomaga w rozwijaniu umiejętności analitycznych.
- Mogą być z powodzeniem stosowane w zajęciach z matematyki.
- Służy jako efektowna forma wprowadzenia do bardziej złożonych tematów.
Jak skutecznie podejść do rozwiązywania zagadek?
Skuteczne podejście do rozwiązywania zagadka z brakującą złotówką wymaga cierpliwości i analizy. Strategie rozwiązywania powinny obejmować jasne zrozumienie wszystkich elementów zagadki oraz umiejętność ich logicznego zestawienia. Kluczowe jest także, aby zadawać pytania i nie bać się myśleć krytycznie.
Unikanie błędów jest równie ważne. Warto być ostrożnym przy dodawaniu i odejmowaniu kwot, a także uważnie analizować założenia, które przyjmujemy. Często drobne nieścisłości mogą prowadzić do znaczących błędów w obliczeniach, dlatego warto stawiać na precyzyjność.
Zachęta do dalszego rozwijania umiejętności matematycznych
Rozwiązywanie zagadek matematycznych, takich jak zagadka z brakującą złotówką, to doskonały sposób na rozwijanie umiejętności i zachęcanie do samodzielnego myślenia. Warto angażować się w różne formy łamigłówek i ćwiczyć myślenie krytyczne. Dzięki temu nie tylko poprawicie swoje umiejętności matematyczne, ale również nauczycie się efektywnie podejmować decyzje w życiu codziennym.
Najważniejsze wnioski z analizy zagadki z brakującą złotówką
Analiza zagadka z brakującą złotówką pozwala zrozumieć, że mylne postrzeganie sytuacji wynika z błędnego zestawienia kwot oraz pominięcia długów w obliczeniach. Kluczowe jest rozróżnienie między posiadanymi pieniędzmi a zobowiązaniami wobec rodzeństwa, co ukazuje, że nie ma faktycznej "brakującej" złotówki. Przykłady, takie jak sytuacja z pizzą, dodatkowo potwierdzają, jak łatwo można się pogubić w liczbach, co czyni te zagadki fascynującymi i edukacyjnymi.
W kontekście edukacji matematycznej, zagadka z brakującą złotówką jest niezwykle wartościowym narzędziem do rozwijania umiejętności krytycznego myślenia oraz analizy logicznej. Uczniowie mogą korzystać z tej łamigłówki, aby lepiej zrozumieć zasady matematyki i unikać pułapek w myśleniu. Ponadto, wizualizacje i diagramy pomagają w uchwyceniu powiązań między długiem a posiadanymi pieniędzmi, co stanowi ważny krok w kierunku pełnego zrozumienia problematyki.
Warto również pamiętać, że krytyczne myślenie w matematyce jest kluczowe dla rozwiązywania nie tylko zagadek, ale i codziennych problemów finansowych. Poprzez praktykę z różnorodnymi łamańcami językowymi i matematycznymi, można znacząco poprawić swoje umiejętności analityczne, co przyniesie korzyści w wielu aspektach życia. Zachęta do dalszego rozwijania tych umiejętności jest nie tylko potrzebna, ale wręcz niezbędna w dzisiejszym świecie, pełnym złożonych wyzwań matematycznych.